本文所有知识来源:《深入浅出 HTTPS》
该文记录自己的读书情况以及思考
前置知识
-
查看OpenSSL版本
$ openssl version OpenSSL 1.1.1f 31 Mar 2020 -
查看所有OpenSSL支持的命令
$ openssl help -
获取算法的帮助信息
$ openssl rsa --help为了获取更详细的信息,可使用如下命令:
$ man rsa -
构建其它版本的命令行工具
可以在自己指定的工作目录构建一个专属的OpenSSL库,避免和系统的OpenSSL库冲突
# 下载二进制包并解压缩 $ wget https://www.openssl.org/source/openssl-3.0.0-alpha13.tar.gz $ tar xvf openssl-3.0.0-alpha13.tar.gz $ cd openssl-3.0.0-alpha13 # 查看安装手册 $ more INSTALL.md # 查看config $ ./config --help # 安装并编译,安装目录不要和系统目录冲突 执行下面指令需要获取root权限 $ ./config --prefix=/usr/local/openssl --openssldir=/usr/local/openssl $ make $ make test $ make install $ make clean # 运行安装的OpenSSL $ /usr/local/openssl/bin/openssl version wrong 尝试安装3.0.0版本失败 报错说明时缺少相关依赖 cannot open shared object file: No such file or directory
随机数
| 名称 | 生成类型 | 特性 | 说明 |
|---|---|---|---|
| 真正的随机数生成器 | 硬件生成 | 效率高,随机性,不可预测性,不可重现性 | 需要从物理设备获取 |
| 伪随机数生成器 | 软件生成 | 效率高,随机性 | 通过算法获取 |
| 密码学伪随机数生成器 | 软件生成 | 效率高,随机性,不可预测性 | 用于密码学 |
-
工作原理
随机数生成器内维护着一个状态(internal state),对于TRNG来说,内部状态的数值来自于外部设备,称为熵(entropy),比如动态的时间,变化的温度,声音的变化,鼠标位置等;而对于PRNG来说,内部状态的数值来自于模拟的数值,称为种子(seed)。
随机数每次生成随机数的时候,内部状态的值都会变化,这样才能产生不一样的随机数,如果每次熵和种子是一样的,生成的随机数也是相同的,所以熵和种子对于随机数生成来说时非常重要的。
-
OpenSSL命令行工具提供伪随机数
$ openssl rand -base64 24 W/FrOMfrlkdhIc9QpHWPfN9fxZ8Z2D69
Hash算法
概念:
- 加密基元:功能单一,可靠
应用:
- 文件比较
每个文件都有自己独一无二的MD5值 - 身份校验
系统校验用户权限步骤:- 用户输入用户名和口令登录
- 系统使用Hash算法计算出口令的摘要值
- 系统使用用户名和摘要值在数据库表中进行检索,一旦匹配到就说明该用户输入的口令是正确的
安全的密码学Hash算法
-
强抗碰撞性(Collision Resistance)
$$
对任意 (x,x'),有 H(x) = H(x')
$$
如果两个不相同的值能够得到同样的摘要值,表示产生了Hash碰撞。 -
弱抗碰撞性(Second pre-image Resistance)
抗第二原像
$$
已知 x,H(x),求 x' \neq x,有 H(x') = H(x)
$$
给定一个消息和这个消息对应的摘要值,很难找到一条不同的消息也具有相同的摘要值。如果某个算法不符合该特性,表示该算法遇到了second-pre-image(第二原像)攻击。具备弱抗碰撞性的算法必然也具有强抗碰撞性。强抗碰撞性和弱抗碰撞性是相对的概念,强弱并不代表算法的安全程度。
因为很难发生才弱,因为很易发生才强 -----bintou -
单向性(Pre-image Resistance)
原像攻击
给定一个摘要值很难找出它的原始信息,如果计算出了原始信息,则表示该算法遇到了pre-image攻击(attacks)。
$$
已知 y = H(x),求 x
$$
密码学Hash算法都具备单向性。 -
对于攻击者来说,Hash算法的破解难度是 强抗碰撞性 < 弱抗碰撞性 < 单向性
分类
- MD5
- SHA
- SHA-1
- SHA-2
- SHA-3
对称加密算法
- 块密码算法
| 算法 | 密钥长度 | 分组长度 | 说明 |
|---|---|---|---|
| AES | 128,192,256比特 | 128比特 | 对称加密算法的标准算法 |
| DES | 56比特 | 64比特 | 早起对称加密算法标准 |
| 3DES | 128或者168比特 | 64比特 | 三重DES算法 |
| Blowfish | 可变密钥长度,32~448比特之间 | 64比特 | 不推荐使用 |
| Rijndael | 128,192,256比特 | 128,192,256比特 | AES算法的原生算法 |
| Camellia | 128,192,256比特 | 128比特 | 不太常见的加密算法 |
| IDEA算法 | 128,192,256比特 | 128比特 | 不太常见的加密算法 |
| SEED算法 | 128比特 | 128比特 | 不太常见的加密算法 |
- 流密码算法
| 算法 | 密钥长度 | 说明 |
|---|---|---|
| RC4 | 可变密钥长度,建议2048比特 | 目前已被证明不安全 |
| ChaCha | 可变密钥长度,建议256比特 | 一种新型的流密码算法 |
流密码算法
-
一次性密码本(one-time pad)
-
原理:
- 明文与同样长度的序列进行
XOR运算得到密文 - 密文与加密使用的序列再进行
XOR运算就会得到原始明文
- 明文与同样长度的序列进行
-
核心操作:
XOR-
eg:
//明文字符串:good,对应的明文序列如下: 01100111 01101111 01101111 01100100 //密钥字符串:skey,对应的密钥序列如下: 01110011 01101011 01100101 01111001 //加密操作 XOR 01100111 01101111 01101111 01100100 01110011 01101011 01100101 01111001 00010100 00000100 00001010 00011101 //解密操作 00010100 00000100 00001010 00011101 01110011 01101011 01100101 01111001 01100111 01101111 01101111 01100100通过两次异或
XOR操作,最终会得到明文序列
-
-
point:
- 密钥每次必须不一样,否则同一个明文和密钥就会获得相同的内容
- 一次性密钥本是无法破解的,原因在于破解者无法确定破解的明文就是原始序列
-
流密码算法的工作原理(以RC4流密码算法为例):关键在算法内部生成一个伪随机的密钥流(keystream)
密钥流的特点:
- 密钥流的长度和密钥的长度一样
- 密钥流是一个伪随机数,是不可预测的
- 生成伪随机数需要一个种子(seed),种子就是RC4算法的密钥,基于同样一个密钥(或者称之为种子seed),加密者和解密者都能获取相同的密钥流
一旦有了密钥流,可以用XOR运算进行加密解密
流密码算法会在每次XOR运算的时候,是连续对数据流进行运算,每次处理的数据流大小一般是一字节。流密码算法可以并行处理,运算速度非常快,但现在已经不再安全了。
块密码算法
其运算不是一次性完成的,每次都需要对固定长度的数据块(block)进行处理,即完成一次加密或者解密可能要经过多次运算,最终得到的密文长度和明文长度是一样的。
数据块的长度称之为分组长度(block size)。
因为基本明文的长度远远大于分组长度,所以需要经过多次迭代运算才能得到最终的密文或者明文。该步骤称之为迭代模式(Block cipher modes of operation),迭代模式也称为分组模式。每次迭代固定长度的数据块。
分组长度和密钥长度没有必然联系,对称加密算法的安全性取决于密钥长度。
如果明文(或者密文)的长度除以分组长度不是整数倍,需要对明文进行填充,保证最终处理的数据长度是分组长度的整数倍。
迭代模式
| 模式 | 名称 | 特点 | 说明 |
|---|---|---|---|
| ECB | Electronic Codebook | 运算快速,支持并行处理,需要填充 | 不推荐使用 |
| CBC | Cipher Block Chaining | 支持并行处理,需要填充 | 推荐使用 |
| CFB | Cipher Feedback | 支持并行处理,不需要填充 | 不推荐使用 |
| OFB | Output Feedback | 迭代运算使用流密码模式,不需要填充 | 不推荐使用 |
| CTR | Counter | 迭代运算使用流密码模式,支持并行处理,不需要填充 | 推荐使用 |
| XTS | XEX-based tweaked-codebook | 不需要填充 | 用于本地硬盘存储解决方案中 |
填充标准
一般可以用0比特进行填充,但有可能数据本身后面就有0比特。
PKCS#7填充标准
eg:(16进制)
01 1byte==8bit
02 02
03 03 03
04 04 04 04
05 05 05 05 05
06 06 06 06 06 06
规律:可以看出是根据填充的字节数量进行对应的填充
如果填充的字节长度n=3,填充的值为030303;
填充值的最后一个字节代表的就是实际填充的长度 一个字节(byte)等于8比特(bit)
if lth mok k = k-1 -- 01
if lth mok k = k-2 -- 02 02
·····························
if lth mok k = 0 -- k k k k k k .... k
k为分组长度,lth为明文或者密文长度,如果分组长度是256比特,则最多可以填充255个比特。
解密,读取解密值的最后一个字节的值,去除最后n个字节得到原始明文。
PKCS#5 处理范围:8个字节
PKCS#7 处理范围:1~255任意比特
OpenSSL 对称密码
OpenSSL主要使用enc子命令进行加密,可以添加参数指定具体的加密算法,不过也可以使用对称加密算法对应的子命令操作。
# 采用3des算法
$ openssl enc des3
#采用3des算法
$ openssl des3显示系统支持的加密算法
$ openssl list -cipher-algorithms利用OpenSSL进行对称加密实例
AES-256-CBC :表示采用AES算法,密钥长度是256比特,分组模式是CBC
# 执行加密操作
$ openssl enc -aes-256-cbc -salt -in file.txt -out file.enc -pass pass:mypassword -p这条指令会报警告wrong
*** WARNING : deprecated key derivation used.
***警告:已弃用的密钥派生。
消除警告的办法 添加-pbkdf2参数
openssl enc -aes-256-cbc -pbkdf2 -salt -in file.txt -out file.enc -pass pass:mypassword -p控制台输出
salt=BE52F36088617235
key=B97451E6162A4500F28624AD2CEE880B3430B332A15B7E73348189A8A22F105E
iv =4C8A2CF186B37FC9CF118E3E3E92F3B1
指令中各参数意义
-in表示从文件中读出明文内容-out表示将加密内容保存到某个文件中-aes-256-cbc表示加密算法和标准
其中AES算法使用的密钥是通过口令(即mypassword)和 Salt 生成-p参数是打印本次加密过程中salt,密钥,初始化向量的值- AES算法使用的密钥通过口令和 Salt 生成,同样的口令和 Salt 会生成同样的密钥
- Slat 的主要作用是为了保证同样的口令可以生成不同的密钥,是明文传输的
OpenSSL做解密操作
# 解密
$ openssl enc -aes-256-cbc -pbkdf2 -in file.enc -d -pass pass:mypassword -iv 4C8A2CF186B37FC9CF118E3E3E92F3B1 -K B97451E6162A4500F28624AD2CEE880B3430B332A15B7E73348189A8A22F105Ebug and learn:
- bad decrypt 139888977704256:error:06065064:digital envelope routines:EVP_DecryptFinal_ex:bad decrypt:../crypto/evp/evp_enc.c:610:
- EVP Authenticated Encryption and Decryption
消息验证码 MAC
-
特点
- 证明消息没有被篡改,这与Hash算法类似
- 消息是正确的发送者发送的,即消息是经过验证的
-
消息验证码 通信双方维护同一个密钥,只有拥有者才能生成和验证消息验证码
-
模型
$$
MAX值 = mac(消息,密钥)
$$ -
MAC值一般和原始消息一起传输,原始信息可以选择加密或者不加密,通信双发以相同的方式生成MAC值来进行比较。两个MAC值相同表示验证成功,反之失败
-
种类
- CBC-MAC:从块密码算法的CBC分组模式演变而来,最后一个密文分组的值就是MAC值
- HMAC(Hash-based Message Authentication Code):应用在HTTP上很多,算法以Hash算法为加密基元,变种,比如
HMAC-SHA-1,HMAC-SHA256,HMAC-SHA512。
# HMAC伪代码说明
Function hmac
inputs:
key: HMAC 算法的密钥
message: 原始消息
hash: HMAC算法采用的加密基元
blockSize:Hash算法的分组长度
# 要确保密钥长度等于分组长度
if (length(key) > blockSize) then
key <- hash(key)
if (length(key))
key <- Pad(key, blockSize)
# 0x5c * blockSize 的值称为 opad,对 0x5c 迭代多次得到,长度等同于分组长度
# 0x36 * blockSize 的值称为 opad,对 0x36 迭代多次得到,长度等同于分组长度
o_key_pad = key xor [0x5c * blockSize]
i_key_pad = key xor [0x36 * blockSize]
# 进行多次 Hash 运算得到MAC值
return hash(o_key_pad // hash(i_key_pad // message))openssl
# 得到file.txt的摘要值
$ openssl dgst -sha1 file.txt
SHA1(file.txt)= 7e8de2164433aa584f8f639b4e23cf07b5ba8c59
$ openssl sha1 -out digest.txt file.txt
$ cat digest.txt
SHA1(file.txt)= 7e8de2164433aa584f8f639b4e23cf07b5ba8c59# 生成HMAC值
$ openssl dgst -sha1 -hmac "mykey" file.txt
HMAC-SHA1(file.txt)= d0d02cf6639acb07dc6cd1da759144addba09493- 加密算法不能提供完整性(消息没有被篡改)攻击者虽然无法破解数据,但是可以修改密文的部分数据,然后发送给接收者,接收者通过密钥解密,但解密出来的值实际上却不是原文,消息已经被攻击者篡改了,即加密操作不能确保数据的完整性。
将加密和MAC结合起来,能够保证消息同时具备机密性和完整性。
AE加密模式
使用这结合对称加密和MAC算法,提供机密性和完整性的模式也叫Authenticated Encryption (AE)加密模式
- Encrypt-and-MAC (E&M)
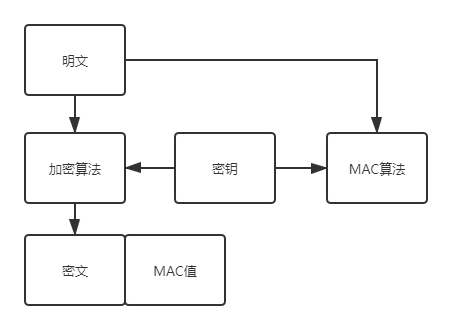
- MAC-then-Encrypt (MtE)
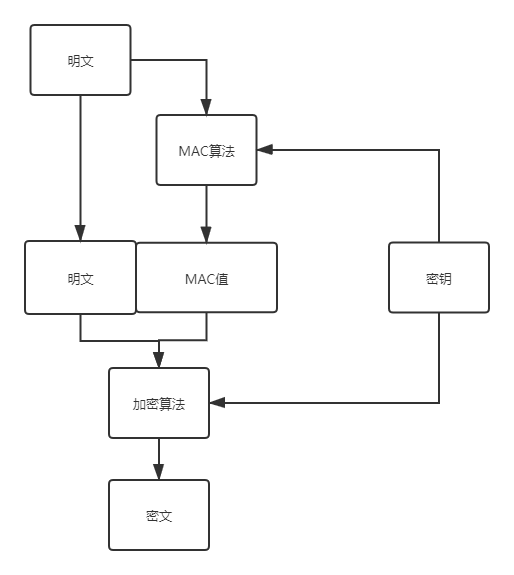
- Encrypt-then-MAC (EtM)
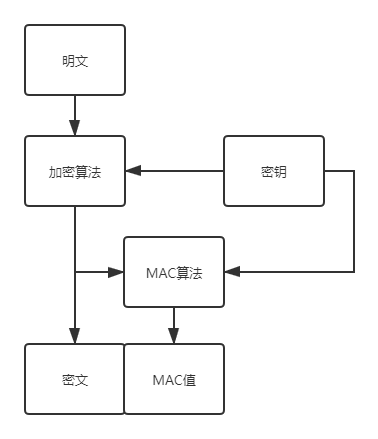
(E&M)和(MrE)使用不当会存在安全问题,目前是建议使用(EtM)模式,而且这三种模式中的加密和MAC操作需要分别处理,一档处理不当,就有可能存在安全风险。
AEAD加密模式
AEAD(Authenticated Encryption with Associated Data)是AE加密模式的一种变体。该模式在底层组合了加密运算和MAC运算,能够同时保证数据机密性和完整性,减轻使用者的负担。
- CCM模式(counter with CBC-MAC)
加密算法:块密码AES-CTR变种算法 / MAC运算:CBC-MAC 在HTTPS中使用少 底层采用(MtE)模式。 - GCM模式(Galois / Counter Mode)
加密算法:块密码AES-CTR变种算法 / MAC运算:GHASH 效率和性能都较好 - ChaCha20-Poly1305 ---谷歌发明
加密算法:ChaCha20流密码算法 / MAC运算:Poly305
公钥密钥算法
RSA
密钥文件(公钥和私钥)内部结构如下
typedef struct rsa_st
{
BIGNUM *p;
BIGNUM *q;
BIGNUM *n;
BIGNUM *e;
BIGNUM *d;
} RSA;生成过程:
- 选取两个很大的质数$p$和$q$
- 计算 $n = p \times q$
- 取一个公开指数$e$,这个数的值小于$(p-1)\times(q-1)$,e对应的值和$(p-1)\times(q-1)$的值互质。
- $e$和$n$组合起来即公钥,$n$的长度就相当于密钥对的长度。
- 通过$e$,$p$,$q$能够计算出私钥$d$,$d$和$n$组合起来即私钥。$e$和$d$存在互逆的关系。
-
RSA加密
$$
C = M^e \pmod {n}
$$ -
RSA解密
$$
M=C^d \pmod {n}
$$ -
加密和解密互逆
$C^d的过程相当于(M^e)^d$
$(M^e)^d相当于M^{e*d}$
$ (e*d) \mod n ==1 $
$ C^d \pmod n 最终能反解出M$
幂运算的逆过程即求对数问题,模运算是离散问题,所以RSA是一个离散对数问题,只要$n$的长度足够长,离散对数很难破解。
攻击手段
- 公钥持有人有$e$和$n$,需要计算出$d$,前提是计算出来$p$和$q$,想要因式分解一个大数$n$是一件困难的事情,暴力破解很难。
- 攻击者想从密文和公钥破解私钥,就要解决离散对数问题,这也是件困难的事情。
现今,对于RSA算法来说,一个2048比特长度的密钥被认为是安全的。
RSA应用
-
单步加密
-
双向加密 --但性能不好
openssl
使用genrsa子命令生成密钥对(文件)
# 生成的密钥长度是2048比特
$ openssl genrsa -out mykey.pem 2048
# 口令结合3DES算法保护密钥对
$ openssl genrsa -des3 -out mykey2.pem 2048从密钥对中分离出密钥
$ openssl rsa -in mykey.pem -pubout -out mypubkey.pem
# 需要输入口令才能分离出公钥 -pubout 即输出一个公钥文件
$ openssl rsa -in mykey2.pem -pubout -out mypubkey2.pem校验密钥对文件是否正确
# -noout表示不打印密钥对信息
$ openssl rsa -in mykey.pem -check -noout显示公钥信息
Modulus的值表示公开密钥系数,即$n$
Exponent的值表示公钥,即$e$
# -in参数表示输入文件
# -pubin表示输入的是公钥文件
# -text参数表示打印密钥的相关信息
$ openssl rsa -pubin -in mypubkey.pem -text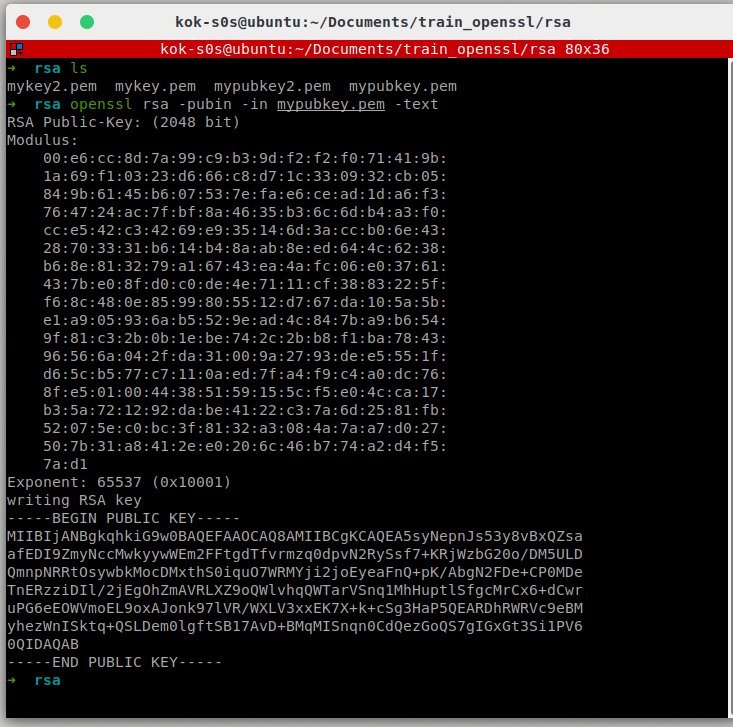
RSA加解密
rsautl命令默认的填充机制是PKCS#1 v1.5,也可以指定使用PKCS#1 OAEP,在命令末尾加上-oaep即可
$ openssl rsautl -encrypt -inkey mykey.pem -in plain.txt -out cipher.txt -oaep$ echo "hello" >> plain.txt
# 使用密钥对加密
$ openssl rsautl -encrypt -inkey mykey.pem -in plain.txt -out cipher.txt
# 使用公钥加密
$ openssl rsautl -encrypt -pubin -inkey mypubkey.pem -in plain.txt -out cipher.txt
# 解密
$ openssl rsautl -decrypt -inkey mykey.pem -in cipher.txt密钥
密钥的特性:
- 足够的长度
- 不可预测性
生成密钥的方式:
- 基于伪随机生成器生成密钥
- 基于口令的加密(Password-based Encryption,PBE)算法产生密钥
PBE算法生成的密钥一般无需存储,因为使用同样的口令能够生成同样的密钥。
口令
password / passphrase 容易生成,易于记忆,弱密钥,由固定的字母,数字,符号组成,长度上有限制
可以用字典进行攻击
作用:口令用于身份校验
PBKDF2算法 ---(RFC2898文档)
openssl
# enc子命令
$ openssl enc -aes-256-cbc -salt -in file.txt -out file.enc -pass pass:password -p使用enc时,会基于口令和salt生成一个对称加密算法强密钥-pass pass:password -p。
# genrsa子命令
$ openssl genrsa -des3 -out mykey.pem 2048使用genrsa子命令生成RSA密钥对的时候,为了防止该密钥对被泄露,可以使用对称加密算法进行保护。对称加密算法使用的密钥就是通过口令生成的。
- 静态密钥
- 动态密钥
密钥协商算法
可以解决密钥分配,存储,传输等问题
RSA密钥协商算法
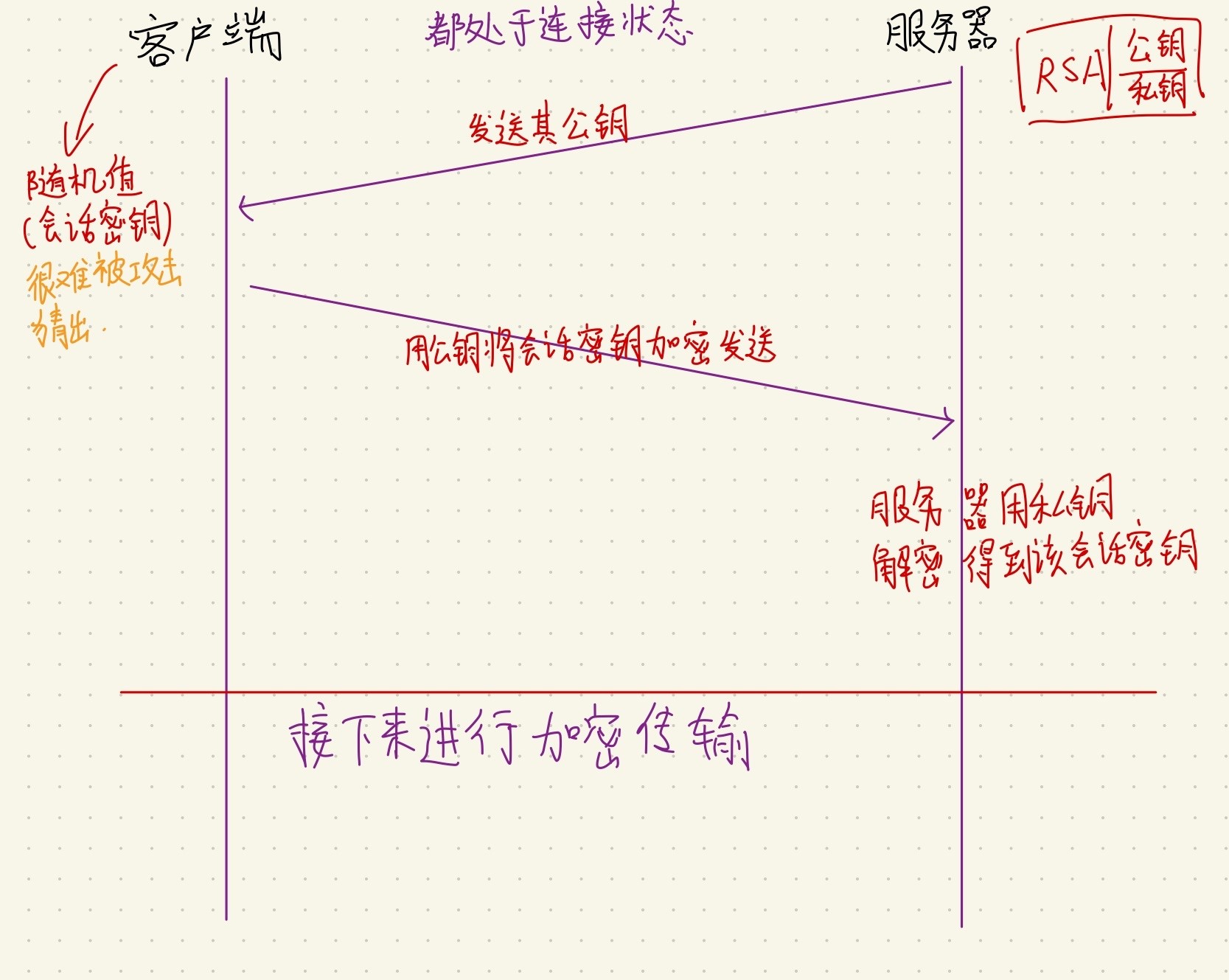
优点:
- 每次连接阶段的会话密钥是不同的,无须存储到设备中,连接关闭后会话密钥就会消失。
- 每次连接中的会话密钥是不同的,避免了烦琐的会话密钥分配问题。
- 虽然RSA运算很慢,但由于会话密钥长度相对很小,计算的数据量并不大,所以性能消耗相对可控。
缺点:
- 获取会话密钥过程不是一个协商过程,只是单方面由客户端来决定的,只能称之为密钥传输。如果客户端生成会话密钥没有使用标准的算法,会带来安全隐患。eg:客户端每次随机从26个字母中选取4个字母作为会话密钥,那么很容易受到暴力攻击。攻击者不会去破解RSA加密算法的私钥,直接暴力破解会话密钥就能反解出明文。
- 不能提供前向安全性。
DH密钥协商算法
Diffie-Hellman
参数文件
typedef struct dh_st
{
BIGNUM *p; //质数
BIGNUM *g; //生成元
//DH 密钥对
BIGNUM *pub_key;
BIGNUM *priv_key;
} DH;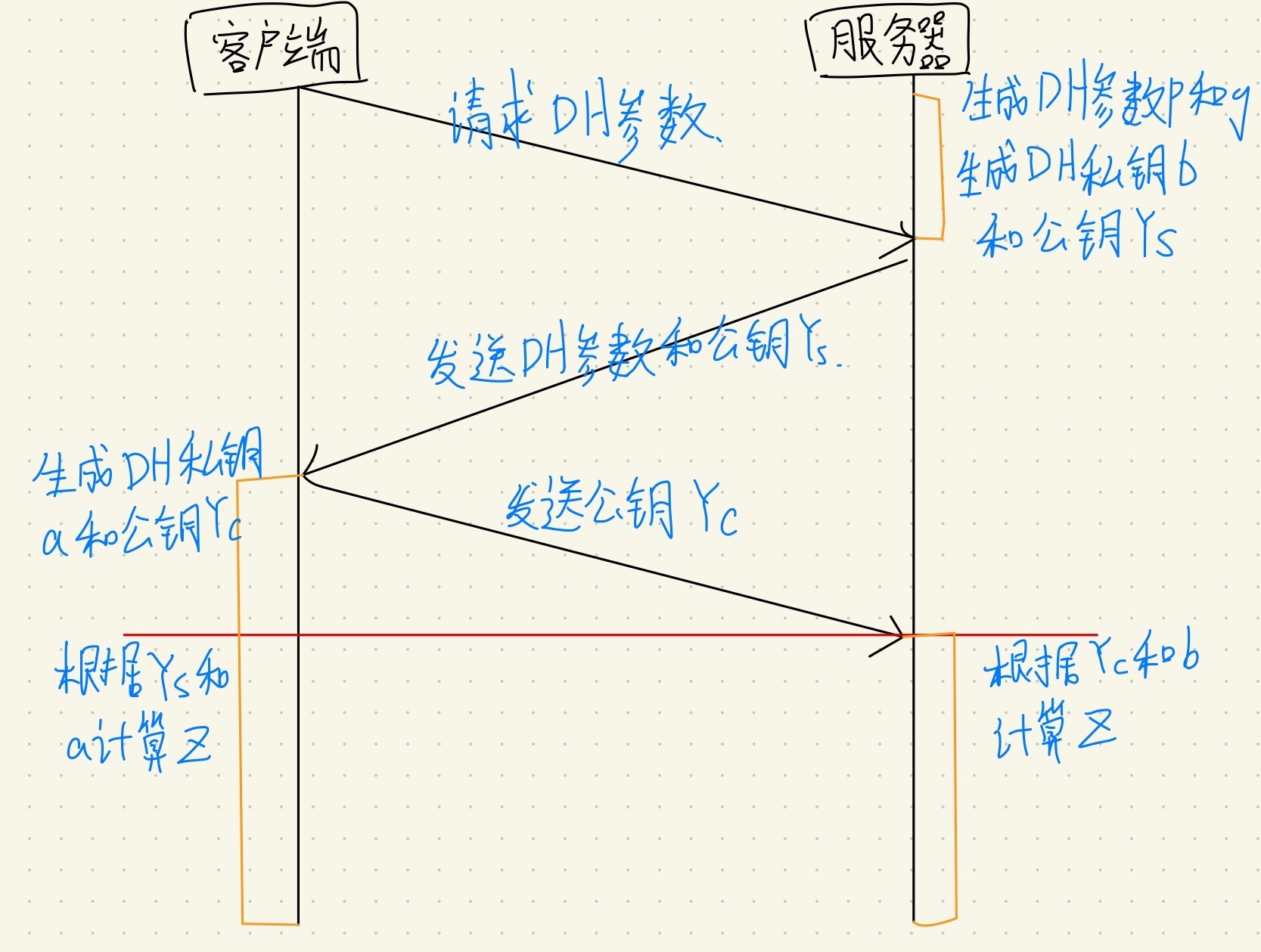
破解DH的密钥,要面临离散对数和因式分解问题,所以保证一定的密钥长度,DH算法就会具有很高的安全性,也能够有效避免攻击。
分类
- 静态DH算法(DH算法) p,g固定 Ys固定 但服务器对应的DH私钥泄露,就无法提供前向安全性 该算法能够避免在初始化连接时频繁生成参数p和g,该过程非常消耗CPU运算。
- 临时DH算法(EDH算法) 有限的时间,有效的空间内生成了密钥对。
openssl
dhparam和genpkey子命令
DH密钥对生成方式:1. 先生成参数文件;2.根据参数文件生成密钥对;
同一个参数文件可以生成无数多且不重复的密钥对
# 生成一个1024比特的参数文件
$ openssl dhparam -out dhparam.pem -2 1024
# 查看参数文件内容
$ openssl dhparam -in dhparam.pem -noout -C
# 基于参数文件生成密钥对
$ openssl genpkey -paramfile dhparam.pem -out dhkey.pem
# 查看密钥对文件内容
$ openssl pkey -in dhkey.pem -text -noout完整的协商例子
# 通信双方的任何一方生成DH的参数文件,可以对外公开
$ openssl genpkey -genparam -algorithm DH -out dhp.pem
# 查看参数文件的内容,包括p和g等参数
$ openssl pkeyparam -in dhp.pem -text
# 发送方A基于参数文件生成一个密钥对
$ openssl genpkey -paramfile dhp.pem -out akey.pem
# 查看密钥对内容
$ openssl pkey -in akey.pem -text -noout
# 发送方B基于参数文件生成一个密钥对
$ openssl genpkey -paramfile dhp.pem -out bkey.pem
# 查看密钥对内容
$ openssl pkey -in bkey.pem -text -noout
# 发送方A拆出公钥文件akey_pub.pem,私钥自己保存
$ openssl pkey -in akey.pem -pubout -out akey_pub.pem
# 发送方B拆出公钥文件bkey_pub.pem,私钥自己保存
$ openssl pkey -in bkey.pem -pubout -out bkey_pub.pem
# 发送方A收到B发送过来的公钥,将协商出的密钥保存到data_a.txt文件
$ openssl pkeyutl -derive -inkey akey.pem -peerkey bkey_pub.pem -out data_a.txt
# 发送方B收到A发送过来的公钥,将协商出的密钥保存到data_b.txt文件
$ openssl pkeyutl -derive -inkey bkey.pem -peerkey akey_pub.pem -out data_b.txt
该实例中,客户端和服务器端每次生成的密钥对都是不一样的,即能提供前向安全性。(临时DH算法)
椭圆曲线密码学
优点:安全性,极短的密钥能够提供很大的安全性。
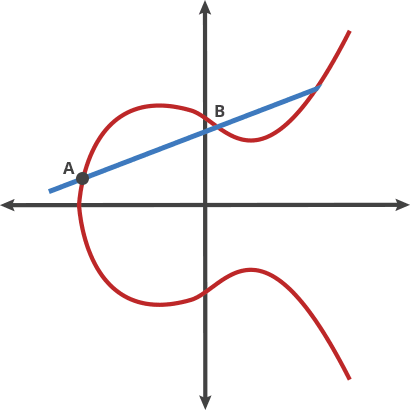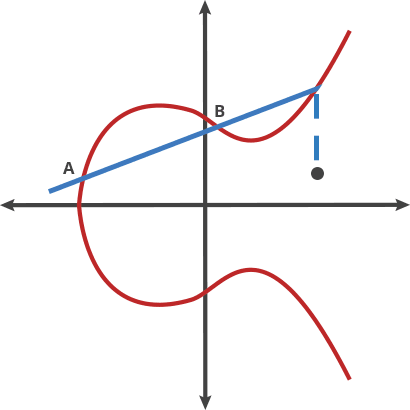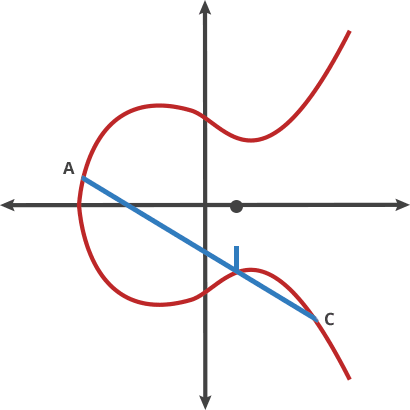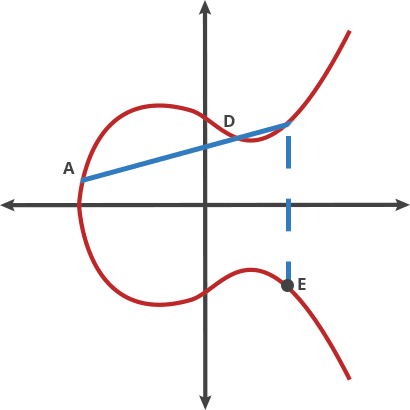
ECC:方程式 | 基点(G) | 质数(P) | a | b
命名曲线 (name curve) eg:secp256k1
每个命名曲线都有唯一的参数文件
建议使用NIST标准建立的命名曲线
openssl
# 查看系统有多少椭圆曲线,通信双方需要选择一条都支持的命名曲线
$ openssl ecparam -list_curves
# 生成一个参数文件,通过 -name 指定命名曲线
$ openssl ecparam -name secp256k1 -out secp256k1.pem
# 默认的情况下,查看参数文件只会显示曲线的名称
$ openssl ecparam -in secp256k1.pem -text -noout
ASN1 OID: secp256k1
# 显示参数文件参数
$ openssl ecparam -in secp256k1.pem -text -param_enc explicit -nooutECDH协商算法
# 生成参数文件
$ openssl ecparam -name secp256k1 -out secp256k1.pem
# A 和 B 各自生成一个 ECDH 私钥对文件
$ openssl genpkey -paramfile secp256k1.pem -out akey.pem
$ openssl genpkey -paramfile secp256k1.pem -out bkey.pem
# A 和 B 分解出公钥,将公钥发送给对方
$ openssl pkey -in akey.pem -pubout -out akey_pub.pem
$ openssl pkey -in bkey.pem -pubout -out bkey_pub.pem
# A 和 B 计算出同样的会话密钥
$ openssl pkeyutl -derive -inkey akey.pem -peerkey bkey_pub.pem -out data_a.txt
$ openssl pkeyutl -derive -inkey bkey.pem -peerkey akey_pub.pem -out data_b.txt 数字签名
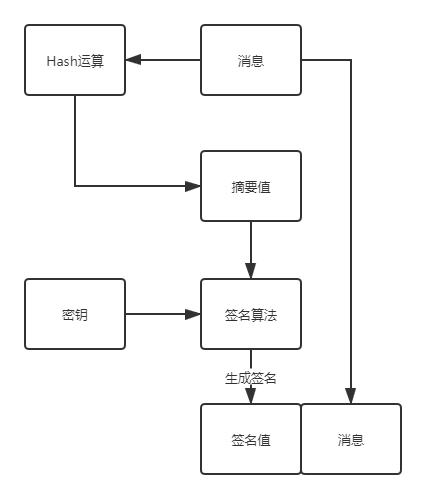
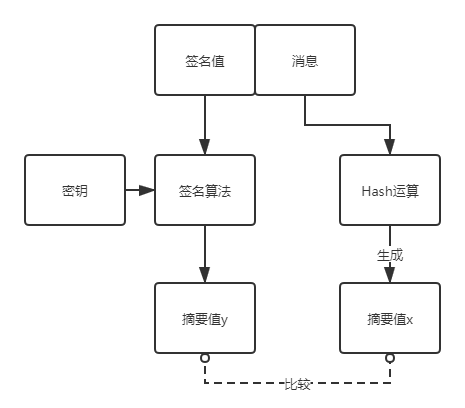
签名值除了做比较无其它用途,基于消息生成签名和基于摘要值生成签名无区别,而且公开密钥算法运行是相对缓慢的面,对消息摘要值(该值长度固定)进行签名,运算时速度会比较快。
RSA数字签名实践(openssl)
-
使用 RSAES-PKCS1-V1_5 标准
# 生成一个 RSA 密钥对,密钥长度 1024 比特 $ openssl genrsa -out rsaprivatekey.pem 1024 # 从密钥对中分离出公钥 $ openssl rsa -in rsaprivatekey.pem -pubout -out rsapublickey.pem # 对 plain.txt 文件使用 sha256 Hash 算法和签名算法生成签名文件 signature.txt $ echo "hello" >>plain.txt $ openssl dgst -sha256 -sign rsaprivatekey.pem -out signature.txt plain.txt # 用相同的摘要算法和签名算法校验签名文件,需要对比签名文件和原始文件 $ openssl dgst -sha256 -verify rsapublickey.pem -signature signature.txt plain.txt -
使用 RSASSA-PSS 标准
# 生成 RSA 密钥对 $ openssl genrsa -out rsaprivatekey.pem 1024 $ openssl rsa -in rsaprivatekey.pem -pubout -out rsapublickey.pem # 指定 RSASSA-PSS 标准 $ openssl dgst -sha256 -sign rsaprivatekey.pem -sigopt rsa_padding_mode:pss -out signature.txt plain.txt # 验证签名 $ openssl dgst -sha256 -verify rsapublickey.pem -sigopt rsa_padding_mode:pss -signature signature.txt plain.txt
DSA数字签名算法
数字签名技术 标准DSS(Digital Signature Standard)
标准算法DSA (Digital Signature Algorithm)
内部结构
typedef struct dsa_st
{
BIGNUM *p;
BIGNUM *q;
BIGNUM *g;
BIGNUM *pub_key;
BIGNUM *priv_key;
} DSA;公开参数:p / q / g
p是一个很大的质数,长度很关键,可以在512比特~1024比特之间,但必须是64比特的倍数,其实一般建议该长度大于等于1024比特,p-1必须是q的倍数;
q的长度必须是64比特;
g是一个数学表达式的结果(取决p和q);
步骤
- 生成DSA密钥对
- 选取一个随机数作为私钥x,0 < x <q;
- 基于私钥生成公钥$y = g^x mod p$;
- 签名生成
- 生成一个随机数k,1 < k <q;
- 计算$r = (g^k\pmod p) \mod q$;
- 计算$s = (k^{-1} * (H(m)+xr)) \mod q$,H是特定的摘要算法;
- 签名值就是
(r,s),随同原始信息m一起发送;
- 签名验证
- 假如r和s大于q或者小于0,则验证直接失败;
- 计算$w = s^{-1} \mod q$;
- 计算$u1 = H(m)·w \mod q$;
- 计算$u2 = r·w \mod q$;
- 计算$v = (g^u1 * y^u2 \mod p) \mod q$;
- 如果v等于r,则签名验证成功,否则失败;
DSA算法实践
- 生成参数文件和密钥对文件
# 生成参数文件,类似于 DH 参数文件一样
$ openssl dsaparam -out dsaparam.pem 1024
# 通过参数文件生成密钥对 dsaprivatekey.pem
$ openssl gendsa -out dsaprivatekey.pem dsaparam.pem
# 对私钥使用 des3 算法进行加密
$ openssl gendsa -out dsaprivatekey2.pem -des3 dsaparam.pem
# 通过密钥对文件拆分出公钥
$ openssl dsa -in dsaprivatekey.pem -pubout -out dsapublickey.pem - 显示文件的信息
# 包括三个公共参数、公钥、私钥
$ openssl dsa -in dsaprivatekey.pem -text
# 公钥信息
$ openssl dsa -pubin -in dsapublickey.pem -text - 生成和验证签名
$ echo "hello" >plain.txt
# 进行签名,可以查看 signature.txt 可以发现有原始信息 hello
$ openssl dgst -sha256 -sign dsaprivatekey.pem -out signature.txt plain.txt
# 验证签名
$ openssl dgst -sha256 -verify dsapublickey.pem -signature signature.txt plain.txt
Verified OKECDSA算法
- 直接生成 ECDSA 私钥
$ openssl ecparam -name secp256k1 -genkey -out ecdsa_priv.pem - 显示私钥信息
$ openssl ec -in ecdsa_priv.pem -text -noout- 拆分密钥对获取公钥
# 生成私钥对应的公钥
$ openssl ec -in ecdsa_priv.pem -pubout -out ecdsa_pub.pem
# 显示公钥信息
$ openssl ec -in ecdsa_pub.pem -pubin -text -noout- 生成签名值
$ echo "hello" >>plain.txt
# Hash 算法使用 sha256 算法
$ openssl dgst -sha256 -sign ecdsa_priv.pem -out signature.txt plain.txt - 校验签名
$ openssl dgst -sha256 -verify ecdsa_pub.pem -signature signature.txt plain.txt
Verified OK算法安全性和性能
密钥长度与算法安全性
安全与性能的关键要素:密钥长度
理论上密钥长度越长就越难被攻击,但密钥长度越长运算性能就会下降。
三个主流算法的密钥长度
| 对称加密算法密钥长度 | 公开密钥算法密钥长度 | ECC椭圆曲线密钥长度 |
|---|---|---|
| 80比特 | 1024比特 | 160比特 |
| 112比特 | 2048比特 | 224比特 |
| 128比特 | 3248比特 | 256比特 |
| 192比特 | 7680比特 | 384比特 |
| 256比特 | 15360比特 | 512比特 |
横向对比,安全性是大致差不多的。
推荐密钥长度
| 密码学算法 | 推荐的密钥安全长度 |
|---|---|
| AES对称加密算法 | 128比特 |
| RSA加密和签名算法 | 2048比特 |
| DSA数字签名算法 | 2048比特 |
| ECC椭圆曲线 | 256比特 |
密码学性能测试
使用OpenSSL中的speed能够测试速度,能了解到不同密码学的性能,但测试的结果并不是有多准确。